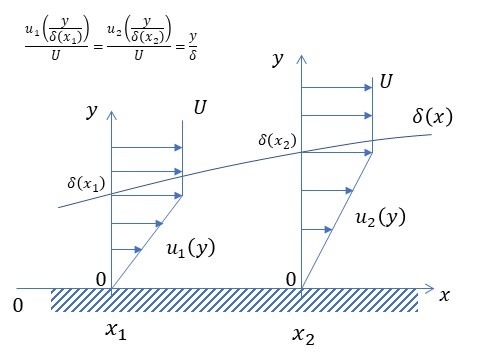
一様速度 U m/s の流れに置かれた平板上で境界層が図のようにに発達しているとする.
境界層内の速度分布は,境界層の厚みを \( \delta \left( x \right) \) とすれば $$ \frac{u_1 \left(\frac{y}{\delta \left( x_1 \right)}\right)}{U}=\frac{u_2 \left(\frac{y}{\delta \left( x_2 \right)}\right)}{U}=\frac{y}{\delta\left( x \right)} $$ と表せる.以下の問いに答えなさい. |