Example(H01)

１時間後にページが自動更新されます。

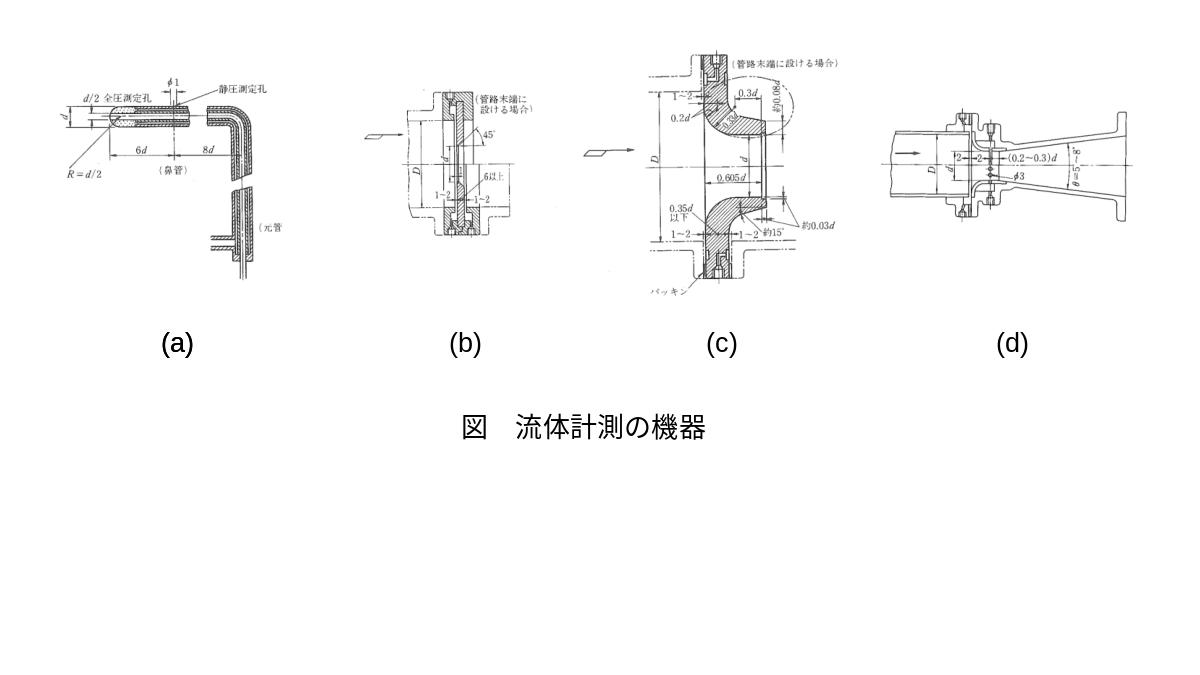
流速・流量計測器

学籍番号

氏　　名

以下の説明文の空白に入る語句を以下の選択肢より選びなさい．

(1) 下図の(a)は()という．一様流れの中におき,流れの\( \boxed {1} \)()と\( \boxed {2} \)()を計測する.
\( \boxed {1} \)と\( \boxed {2} \)から()が求まり,一様流れの流速を計測する.

(2) 下図の(b)は(),(c)は(),(d)は()という.いずれの計測部も管断面積よりも小さくなっており,
その前後に生じる圧力（静圧）差から管内流量を見いだす.
これらの流量計はその計測機構・原理から.\( \boxed {1} \)()流量計、または\( \boxed {2} \)()流量計とよばれる.

(3) \( \boxed {1} \)および\( \boxed {2} \)の流量計測原理は,管断面積 \( A_D \) ( 直径 \( D \) ) からより小さな断面積 \( A_d \) ( 直径 \( d \) ) を管路中に設けることで
管断面平均流速を \( V_D \) から \( V_d \) に加速させる.
これに伴い静圧は \( p_D \) から \( p_d \) に()する.水平に置かれた管を流れる流体において損失のない理想的な流れでは,
()の式\[ \frac{p_D}{\rho} + \frac{V_D^2}{2} \,=\, \frac{p_d}{\rho} + \frac{V_d^2}{2} \]()の式\[ Q \,=\, V_D A_D \,=\, V_d A_d \]より,\( Q \,=\, \)()\( \times \)()\( \times A_d \)となる.

選択肢

(1)	\(\Large \frac{1}{\sqrt{1-(A_D/A_d)^2}}\)	(2)	\(上昇\)	(3)	\(静圧式\)	(4)	\(\Large \frac{1}{\sqrt{1-(A_d/A_D)^2}}\)
(5)	\(JIS標準型ピトー管（L型）\)	(6)	\(JIS標準型オリフィス\)	(7)	\(ベルヌーイ\)	(8)	\(\Large \sqrt{\frac{2}{\rho}(p_D-p_d)}\)
(9)	\(\Large \sqrt{\frac{2}{\rho}(p_d-p_D)}\)	(10)	\(差圧式\)	(11)	\(低下\)	(12)	\(動圧\)
(13)	\(JIS標準型ベンチュリ計\)	(14)	\(連続\)	(15)	\(全圧式\)	(16)	\(静圧\)
(17)	\(絞り\)	(18)	\(全圧\)	(19)	\(トリチェリー\)	(20)	\(JIS標準型管ノズル\)
(21)	\(動圧式\)