メニューに戻る

１時間後にページが自動更新されます。

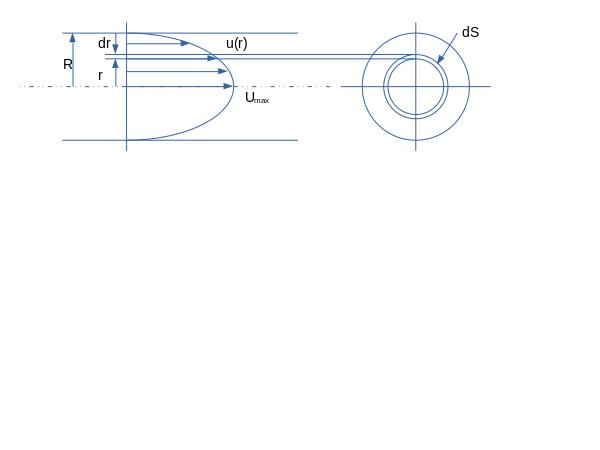
断面を通過する運動量

学籍番号
氏　　名
下図のように半径 R の円管に、動粘性係数 ν= 1.52 \(mm^2/s\) の水が流れている。
円管中央の速度が \(U_{max}\)であるとき,速度分布は
\( \Large \frac{ u(r) }{U_{max}} = 1 - ( \frac{r}{R} )^2 \)
で表せる．断面を毎秒通過する運動量の大きさ (\(N \cdot s\) ) を以下の手順にしたがって求めなさい．
(1) \( r \)の位置に微小面 \(dS \,=\, \) ()×() を考えると,
(2) 微小面\( dS \)を通過する流量は, \(dQ \,=\, \)() \(dS\) なので、
(3) 微小面\( dS \)を通過する運動量は, \(dM \,=\, \)()×() \(dQ\) なので、
(4) 断面全体を毎秒通過する運動量は,\(M \,=\, \int dM = \, \int_{0}^{R} \) ()×()×()×() \( dr \)
(5) 流量を \( Q \),断面平均速度を \( U_{ave} \)と表すと \( M \,=\, \)()×\( \rho Q U_{ave}\) となる．
\( R = 25 mm \), Umax \(= 3.0 cm/s\), \( \rho = 1000.0 kg/m^3 \)であれば、
(6) 断面全体を毎秒通過する運動量は () \( mN \cdot s \)となる．（有効数値3桁で回答すること．）


(1)\(\large R\) (2)\(\large \frac{3}{2}\) (3)\(\large \frac{1}{3}\) (4)\(\large \pi r^2\) (5)\(\large Q\) (6)\(\large U_{max}\)
(7)\(\large \frac{4}{3}\) (8)\(dS\) (9)\(\large dr\) (10)\(dQ\) (11)\(\large \frac{1}{2}\) (12)\(\large \frac{2}{3}\)
(13)\(\large u(r)\) (14)\(\large \rho\) (15)\(\large \pi R^2\) (16)\(\large 2 \pi r\) (17)\(\large 2 \pi R\) (18)\(\large r\)

ヒント：(4)の積分は 変数 \( r \) の積分を変数 \( u \) の積分に置換すると良い．

積分範囲は
\( \Large \frac{r| 0 \Rightarrow R}{u| U_{max}\Rightarrow 0}\)

\( \Large \frac{du}{dr} = - \frac{2r}{R^2} U_{max}\) なので、 \( \Large 2 r dr \) を \( \Large - \frac{R^2}{U_{max}} du\) で置換する．、